4. Dihedral Group

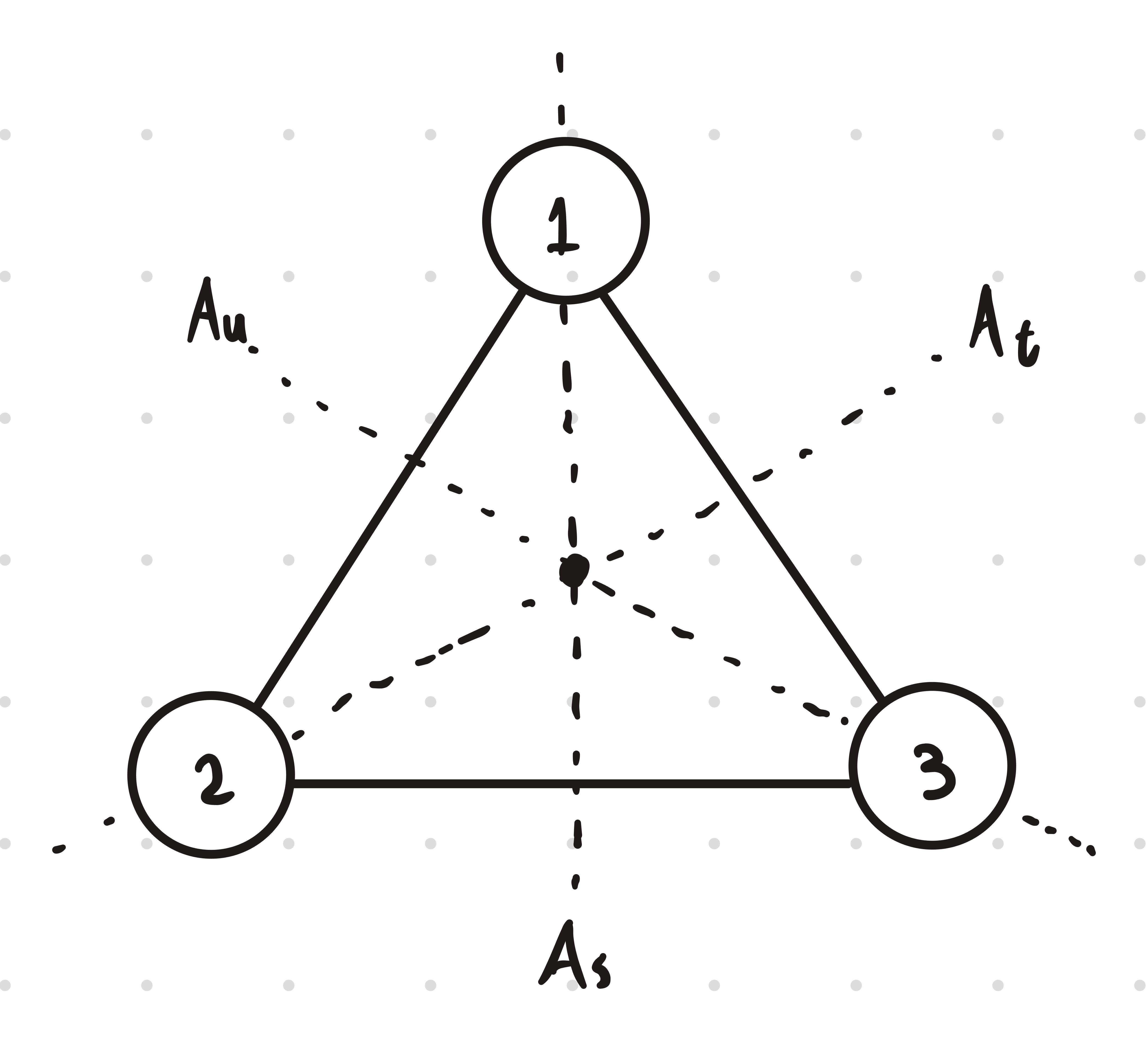
Node Positions

6 unique combinations

$$(1, 2, 3) = Id, \quad (3, 1, 2) = r, \quad (2, 3, 1) = r^2$$ $$(1, 3, 2) = s, \quad (3, 2, 1) = t = rs, \quad (2, 1, 3) = u = r^2s$$

 

Transformation Representation

We can now write all transformations in terms of $r$ and $s$

$$\{\; Id, \; r, \; r^2, \; s, \; rs, \; r^2s \; \}$$

 

Satisfies Composition Rules?

 

Closure

For any $x, y \in G,$ the product $(x \cdot y) \in G$

$$(rs)(r^2s) = r(sr^2)s = r(rs)s = r^2s^2 = r^2$$

 

Associativity

For all elements in $G$, $(x \cdot y) \cdot z = x \cdot (y \cdot z)$

$$(rs)r^2 = r(sr^2)$$

 

Identity

There exists an element $e \in G$ such that $e \cdot x = x \cdot e = x$ for every $x \in G$

$$Id \circ r = r \circ Id \\ \; \\ Id \circ s = s \circ Id$$

 

Inverse

For each $x \in G$, there exists an element $x^{-1} \in G$ such that $x^{-1} \cdot x = x \cdot x^{-1} = e$

$$(rs)(sr) = r(sr)s = r(r^2s)s = r^3s^2 = Id \circ Id = Id$$

 

Summary

• ($D_3$) is the dihedral group of order 6
• It captures all rotations and reflections of an equilateral triangle
• Every group axiom is satisfied, making it a proper mathematical group